Physical properties of glass
Home » Physical properties of glass
There are a number of Physical properties of glass that can be measured.
Viscosity
Viscosity is one of the most important parameters for optimized glass processing. Therefore, it is important to know the viscosity temperature relationship of a glass. Measuring the viscosity is straightforward: a force is applied on the glass sample, the resulting velocity gradient is measured, and the viscosity is calculated.
Several specific viscosities have been designated as reference points for common practical use.
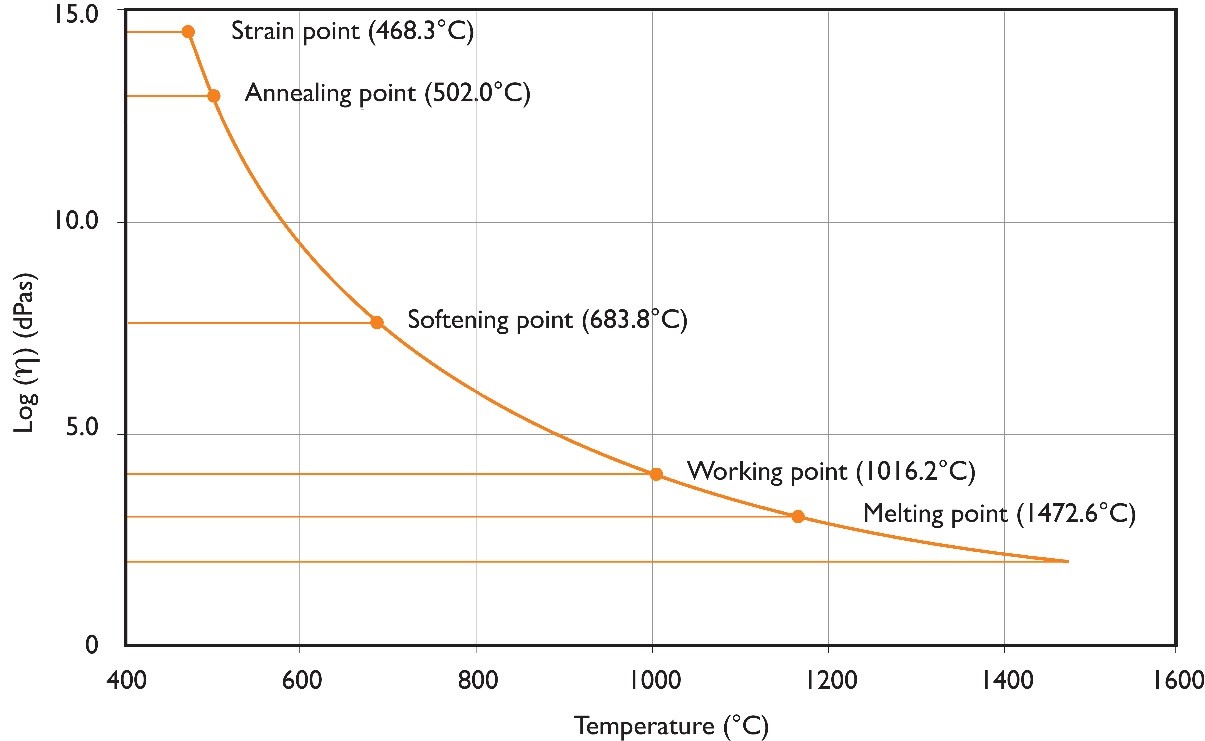
A homogeneous melt can be obtained at the melting point, where viscosity equals 2.0 dPas. The working point is the viscosity at which a melt is delivered to a forming device, typically around 4.0 dPas. The softening point is the minimum viscosity that can prevent the glass from deforming under its own weight on a typical glass working time scale, which corresponds to 7.6 dPas. The temperature range between the working point and the softening point is defined as the working range. After the glass is formed, the internal stresses which result from the glass forming process need to be released by annealing. The annealing point (13.0 dPas) is defined as the temperature where stress is substantially relieved within a few minutes, whereas at the strain point (14.5 dPas) the stress release is achieved within several hours.
A typical viscosity temperature curve for a soda lime glass, containing the characteristic viscosity points, is shown in the Figure above.
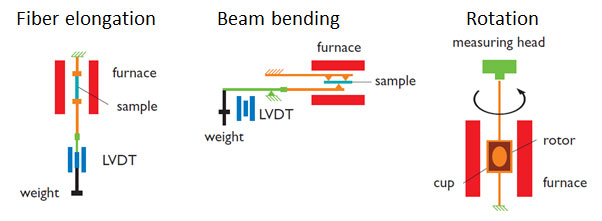
In practice, no single analytical method is capable of measuring the full range of viscosities and/or the entire temperature range. To fully cover this range three methods are available (as illustrated below):
- The fiber elongation method is used for the high viscosity range. The elongation speed of a fiber is determined at different temperatures and using different weights. The viscosity is calculated from the elongation speed.
- The beam-bending method has proven to be of great value in measuring viscosities of quartz glasses in the middle region. The bending speed of a beam is determined at different temperatures and using different weights. The viscosity is calculated from the bending speed.
- A rotation method is applied for the low viscosity range. The shear stress and shear rate of a rotating bob immersed in a cup filled with glass are measured at different temperatures. The viscosity is calculated from the shear stress and shear rate.
The precision is better than 2°C and the accuracy is tuned using appropriate reference materials. To realize accurate and precise results, the temperature gradients in the sample are kept as low as possible.
Thermal expansion behavior and stress
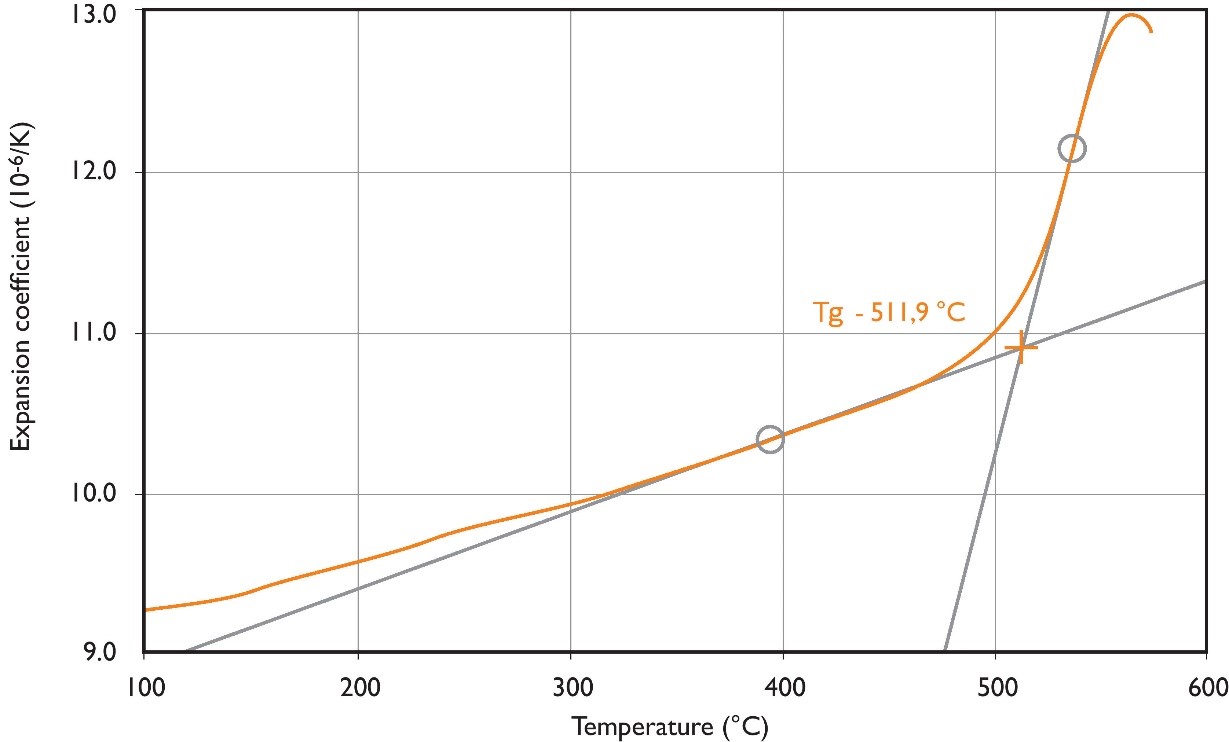
Often glass parts have to be joined with other glasses or even completely different materials (e.g. metals or ceramics) to form the final product. It is of great importance that the thermal expansion behavior of the materials involved are well matched. Thermal expansion coefficients can be accurately measured using a double quartz differential dilatometer. This experimental set-up measures the elongation of a sample as a function of temperature. An example of the resulting expansion coefficient as a function of temperature is shown in the Figure below.
In addition, stress in glass can be measured using the so-called strain slab method. The sample of interest and a standard glass are sealed together and cooled in an oven, using a predefined temperature program. A difference in thermal expansion between the two glasses will yield stress in the seal region. The stress can be quantified by measuring an optical birefringence effect with a polarization microscope.
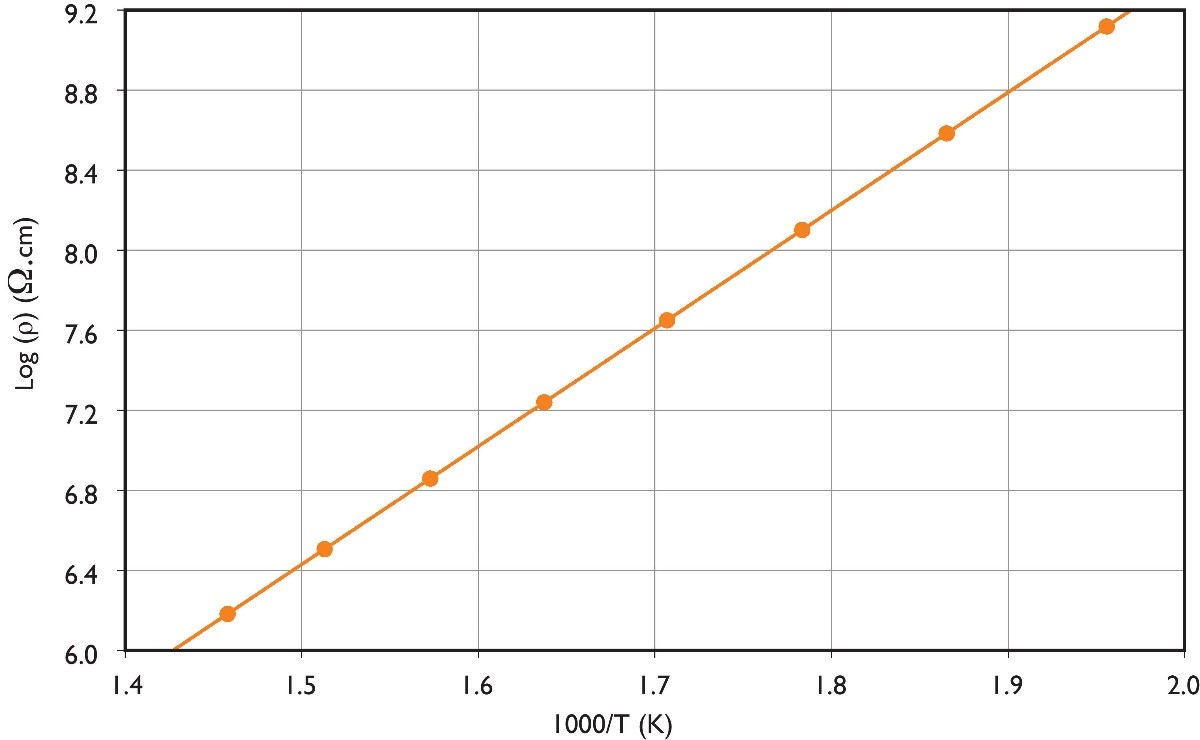
Electrical resistance
In some applications the specific electrical resistance of the glass below the transformation temperature is important. In high voltage applications, for example, a high electric resistivity is required for low leakage currents. An example of the specific resistance (ρ) as a function of temperature is shown in the Figure. Specific resistances can be measured in the range of 105 – 1012 Ωcm with high precision and accuracy.
Optical properties
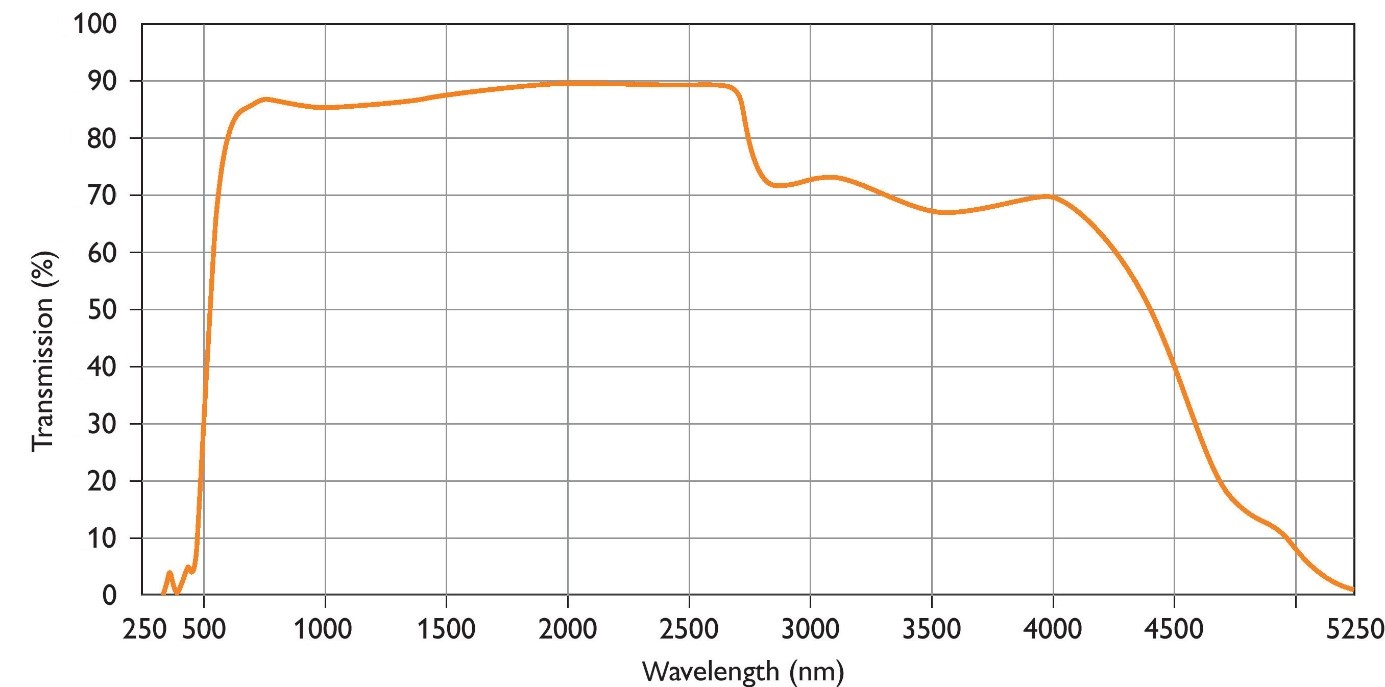
In many applications the optical properties of glass are important. Transmission and reflection properties of glass and finished products can be measured over the entire UV/VIS/NIR/IR wavelength region (175 nm – 16000 nm). An example of light transmission as a function of wavelength is shown.
Transmission measurements can be used to determine the Fe2+/ Fe3+ ratio in glass and the water (β-OH) concentration in quartz glass.
Would you like to learn more about Physical properties of glass?
Contact us today for your physical properties of glass needs. Please complete the form below to have an EAG expert contact you.